COLEGIO PAULO VI
TECNOLOGÍA E INFORMÁTICA
CURSOS: 901 – 902 – 903
DOCENTE: AIDA ELIZABETH MARÍN G.
GUÍA DE TRABAJO
Desempeños1. Representa a través de diagramas algunas secuencias lógicas de programación para la solución de situaciones enunciadas.
2. Reconoce y utiliza operadores lógicos en la programación de algoritmos, usando bloques en la aplicación Scratch.
3. Identifica los componentes de un circuito eléctronico y realiza el montaje de aplicaciones básicas.
SEMANA Marzo 30 a abril 3
En el enlace a continuación encontrarás la definición de algoritmos y diagramas de flujo, igualmente algunos ejemplos al respecto. Lee hasta antes de iniciar el subtítulo ALGORITMO DIRECTOS E INTERACTIVOS
QUE ES UN ALGORITMO Y UN DIAGRAMA DE FLUJO? – CONCEPTO Y EJEMPLOS
Podemos definir, algoritmo como una secuencia ordenada de pasos para resolver un determinado problema. Este concepto se usa mucho en informática, pues siempre debemos «enseñar» al microprocesador como debe ejecutar sus acciones para conseguir, por ejemplo, el cálculo de los materiales de una pared de una viviendas. Este concepto de «enseñar» se denomina PROGRAMAR y para ello se utilizan distintos lenguajes de programación, como Fortran, Dbase, Visual Basic, C++, etc.

En el paso del problema al programa una PC interviene en primer lugar el analista, que se encarga de definir el algoritmo de resolución, y el programador, que traduce dicho algoritmo al lenguaje adecuado a la aplicación de que se trate.
El ejemplo mas fácil para entender este concepto es cuando debemos realizar una comida y no sabemos como se hace. En tal situación para salvar este problema recurrimos a un libro de recetas en donde nos indica paso a paso las accines que debemos realizar para llegar a buen puerto.
Como se vé el término algoritmo no está unido, como podría pensarse, a procesos científicos más o menos complejos, sino que en muchas ocasiones utilizamos algoritmos específicos sin saber que lo estamos haciendo.
En el caso del cocinero antes indicado que sigue al pie de la letra una receta destinada a la elaboración de un plato. Como comprobación, veamos una receta de cocina cualquiera que tendría que seguir un cocinero o cocinera que quisiese elaborar unas albóndigas de queso roquefort.
Para realizar este plato, habría que seguir los siguientes pasos.
• Primer paso: aplastar y mezclar con un tenedor mantequilla y queso roquefort a partes iguales hasta que los dos elementos se incorporen el uno al otro.
• Segundo paso: dejar reposar la mezcla en un sitio frío, hasta que se endurezca.
• Tercer paso: formar con la pasta endurecida pequeñas bolitas del tamaño de una nuez.
• Cuarto paso: pasar las bolitas construidas por un plato grande lleno de pan rallado.
• Quinto paso: colocar las albóndigas en forma de pirámide en un plato y mantenerlas en el refrigerador hasta el momento de servirlas.
A este lista de pasos, lo podríamos llamar algoritmo culinario, como se puede observar, esta receta de cocina no es más que una forma de algoritmo, ya que cumple todas las características que han de tener éstos: por un lado, se trata de una serie de instrucciones muy concretas que en ningún caso presentan ambigüedad, y por otro, aparecen expresadas de una forma secuencial con un número finito de pasos elementales.
Sigamos ahora con una caso mas técnico, supongamos que queremos resolver mediante un ordenador un problema simple, como, por ejemplo, conocer si el número 7.321 es un número primo (*).
(*): primo significa que solo es divisible por el 1 y por si mismo.
Este problema, tal y como lo hemos planteado, estaría claro para una persona, pero no para un ordenador, ya que, recordemos, no se trata de una máquina «inteligente», es decir, «no sabe qué hay que hacer» para averiguar si un número es primo o no.
La siguiente operación podría ser «decir» al ordenador qué es lo que debe hacer para resolver el problema propuesto. Es decir, dar a la máquina una orden como la siguiente: «divide el número 7.321 por todos los números enteros menores que 7.321 y averigua si alguna de estas divisiones es exacta».
Evidentemente la orden es ya mucho más clara; sin embargo, tampoco en este caso sería entendida por la máquina, ya que, como vimos, ésta es de tipo secuencial y por tanto necesita recibir órdenes dadas con un ritmo y un orden determinados.
Un conjunto de acciones de este tipo debería ser entonces de la siguiente forma:
a) Divide el número 7.321 por 2.
b) Si la división es exacta, para; si no, continúa.
c) Divide el número 7.321 por 3.
d) Si la división es exacta, para; si no, continúa, etc., etc.
Un procedimiento de resolución como el anterior, en el que las diferentes instrucciones están dadas paso a paso, recibe el nombre de algoritmo.
Un algoritmo es entonces algo así como una receta de cocina que está formada por una serie de instrucciones consecutivas que, en caso de seguirse, nos llevan al resultado final deseado.
La elaboración de un algoritmo para la resolución de un problema tan fácil como el propuesto en el ejemplo es una tarea relativamente sencilla; sin embargo, al aumentarla dificultad del problema, la complejidad del algoritmo necesario para su resolución aumenta también de forma espectacular, más cuando lo que sí es claro es que no existe ningún algoritmo que permita obtener algoritmos, y esta dificultad radica básicamente en que, como característica propia de todo algoritmo, éste debe estar formado por un número finito de pasos, cada uno de los cuales debe significar una acción perfectamente definida.
El algoritmo del problema es una de las partes más importantes para la resolución del mismo mediante un ordenador, ya que en él se encuentran las instrucciones que, al expresarse primeramente en lenguaje de programación y más tarde en lenguaje máquina, se transformarán en el programa según el cual el ordenador resolverá el problema propuesto.
Algoritmos para juegos: Uno de los muchos juegos que depende de la habilidad de los jugadores y no de la suerte es el denominado de «las quince cerillas». Para comenzar, coloque quince cerillas sobre una mesa. El jugador número uno toma de una a tres cerillas; a continuación el jugador número dos toma de una a tres cerillas, que guarda. Este proceso se sigue repitiendo hasta que no quedan más cerillas, y pierde el jugador que se ve obligado a tomar la última cerilla. La cuestión es la siguiente: ¿existe alguna estrategia que haga que el jugador que comienza pueda siempre forzar a su contrincante a tomar la última cerilla? Un análisis del juego demuestra que el jugador número uno puede obligar al jugador número dos a tomar la última cerilla si realiza las siguientes acciones: Primer movimiento: el jugador número uno toma dos cerillas.
Movimientos sucesivos: si el jugador número dos toma K cerillas (K<= 3), entonces el jugador número uno toma 4-K cerillas, y así hasta que logre dejar a su oponente la última cerilla. Siguiendo este algoritmo, el éxito es seguro.
Movimientos sucesivos: si el jugador número dos toma K cerillas (K<= 3), entonces el jugador número uno toma 4-K cerillas, y así hasta que logre dejar a su oponente la última cerilla. Siguiendo este algoritmo, el éxito es seguro.
EJEMPLOS: DIBUJANDO EL ALGORITMO, EL DIAGRAMA DE FLUJO:
Una de las características básicas que ha de cumplir todo algoritmo destinado a la solución de un problema es su falta de ambigüedad: sus acciones elementales deben estar expresadas de una forma tal que no quede en ellas ninguna posibilidad de duda. Esta premisa hace que los lenguajes naturales -español, inglés, francés, etc- no sean los más apropiados a la hora de expresar un algoritmo, ya que, en general, todos ellos son poco concisos, de tal forma que ciertas expresiones, fuera de un contexto, presentan un alto grado de ambigüedad.
Para evitar en parte este problema, los algoritmos se suelen expresar en un lenguaje gráfico en el cual todo el proceso aparece como un organigrama.
Este método, además de una mayor concisión en la expresión del proceso algorítmico, tiene sobre otros métodos la ventaja de dar una visión global de la estructura básica que posee el algoritmo.
Un organigrama consiste en un gráfico formado por una serie de líneas que conectan entre sí distintas figuras geométricas, cada una de las cuales representa un tipo de instrucción particular. Así, un óvalo representa tanto el comienzo como el fin del algoritmo, un rectángulo indica la existencia de una instrucción cualquiera, y un rombo representa el símbolo de decisión, esto es, el momento en que dentro del algoritmo se pueden tomar dos o más opciones distintas.
En el interior de estos símbolos se escribe taxativamente el tipo de orden que cada uno de ellos representa, y la línea que los une viene marcada con una flecha que indica la dirección en que se desarrolla el algoritmo.
Una de las diferencias esenciales entre este tipo de organigramas, llamados diagramas de flujo, y el lenguaje natural con que se pueden expresar también los algoritmos reside en los puntos de ramificación –toma de decisiones– del algoritmo.
El lenguaje natural es, por su propia naturaleza, secuencial, lo que implica que, en una toma de decisiones, siempre una de ellas antecede a la otra, cosa que no sucede cuanto el algoritmo se representa por medio de un diagrama de flujo en el que del punto de decisión parten simultáneamente las dos o más decisiones posibles. Es decir: los organigramas permiten una visión bidi-mensional del algoritmo, que no existe en el lenguaje natural.
Si suprimimos las distintas figuras geométricas del diagrama de flujo, este adquiere la apariencia de un árbol o grafo que se denomina esqueleto del algoritmo, el cual indica de una forma aproximada el tipo de algoritmo empleado.
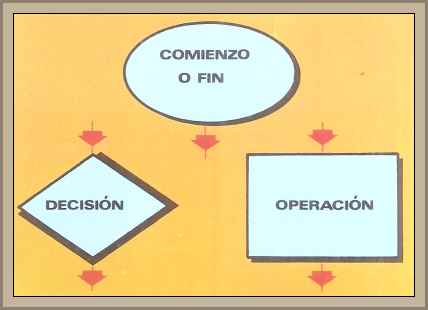
Arriba vemos tres simbolos para dibujar un diagrama de flujo. Combinando esos tres podemos dibujar cualquier razonamiento.
Ejemplo 1: Veamos el ejemplo del número primo:
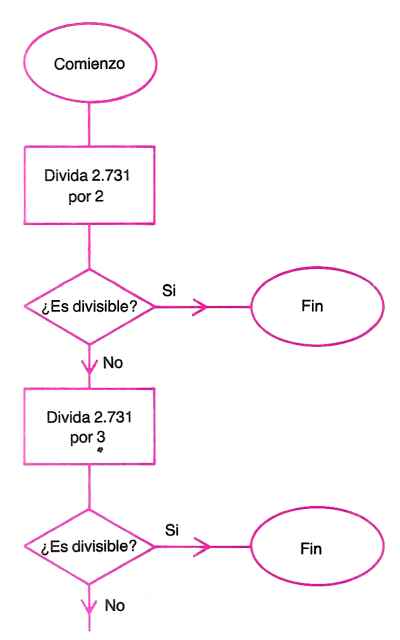
Diagrama de flujo del algoritmo destinado a determinar si el número 2.731 es un número primo. Este algoritmo, aun estando bien definido,
es poco eficiente, pues, por ejemplo, si el número no es divisible por 2, ya no es necesario probar con ningún número par.
es poco eficiente, pues, por ejemplo, si el número no es divisible por 2, ya no es necesario probar con ningún número par.
Ejemplo 2: Algoritmo para cambiar una rueda de una auto:
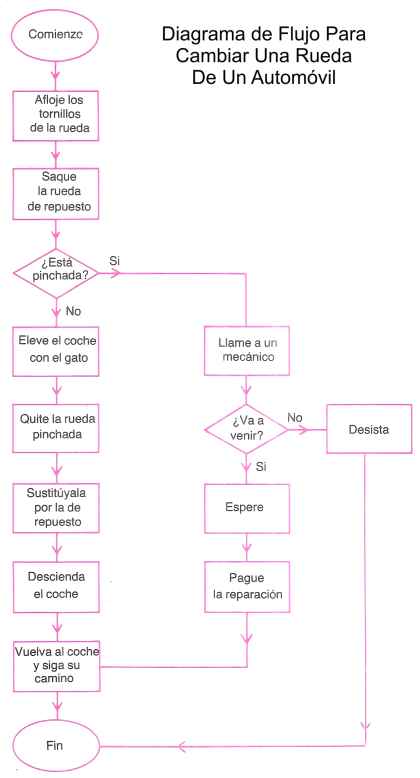
El diagrama de flujo muestra un algoritmo destinado a solucionar un problema común: el pinchazo de una rueda del coche. Como se puede observar, en él se detallan una serie de pasos elementales que se han de realizar en un orden secuencial. Aunque, por razón de extensión, no están señalados todos los pasos posibles, cada uno de los marcados significa una instrucción en la que no existe ambigüedad.
Actividad
1. Realiza en tu cuaderno un cuadro sinóptico sobre la información contenida en el enlace.
SEMANA 2
Realiza el algoritmo para cada una de las siguientes actividades diarias
- Escribe el algoritmo de las actividades que realizas para ir a la escuela desde que despiertas por la mañana.
- Cambiar la llanta pinchada de un automóvil.
- Determinar si una persona es mayor que otra
- Cocinar un huevo.
- Consultar los símbolos para la construcción de diagramas de flujo.
SEMANA 3
Elaboración de diagramas de flujo
6 pasos para hacer un diagrama de flujo de proceso
Como se puede ver, se trata de una representación más simple, que se detallará más adelante, a medida que vayamos avanzando hacia el modelado del proceso.
1. Determine los principales componentes del proceso.
En este paso es necesario aclarar cuáles son las entradas del proceso y sus salidas, así como las actividades que se desarrollan en el mismo.
Las entradas también se denominan inputs y pueden ser recursos, información y otros elementos que “alimentan” el proceso.
Del mismo modo, las salidas (outputs) son los productos generados por el proceso y también pueden ser informaciones, decisiones, permisos, insumos para otros procesos, partes de productos, componentes, servicios, productos terminados, etc.
2. Ordene las actividades
El diagrama de procesos de negocio es un flujo, por lo que se necesita ordenar estas actividades. Haga una lista en orden cronológico.
3. Elija los símbolos correctos para cada actividad
Hay varias notaciones usadas para dibujar diagramas de flujos de procesos. Por lo tanto, al indicar correctamente cada tipo de actividad, utilizando los símbolos correctos, será mucho más fácil para cualquiera que esté familiarizado con los símbolos, poder entender el flujo rápidamente.
Las notaciones van desde las más simples a la más compleja, la notación BPMN 2.0. Si usted es un principiante, escoja las notaciones simples, pero si desea profundizarse en el asunto y hacer un trabajo más completo, utilice el BPMN 2.0.
4. Haga la conexión entre las actividades
Para esto se utilizan conectores, normalmente flechas y líneas de puntos, o continuas. Sus significados se describen también en las publicaciones indicadas más arriba. ¡Consúltenos!
¿Quiere saber más acerca de la notación BPMN 2.0? Siga este enlace: http://www.omg.org/spec/BPMN/2.0/
5. Indique el comienzo y el final del proceso
Puede parecer trivial, pero a veces, las personas se olvidan de indicar cuándo el proceso comienza y cuándo termina. Y esta es una información muy importante para establecer límites para los propietarios de los procesos, gerentes y supervisores.
6. Revise su diagrama de procesos de negocios
¿Usted acabó de dibujar su diagrama de flujo de procesos? ¡Ahora será fácil entender si es realmente asi que ocurre! Revíselo, estúdielo nuevamente y asegúrese de que su representación gráfica del proceso aun es adecuada.
Un algoritmo es una secuencia de PASOS LÓGICOS a seguir para resolver un problema de forma escrita.
Un ejemplo para cocinar un huevo para otra persona sería:
- Pregunto si quiere el huevo frito.
- Si me dice que si, lo frio, si me dice que no, lo hago hervido.
- Una vez cocinado le pregunto si quiere sal en el huevo.
- Si me dice que no, lo sirvo en el Plato, si me dice que si, le hecho sal y después lo sirvo en el plato.
Si te fijas los pasos no pueden cambiar su posición. Sería imposible preguntarle si lo quiere frito después de haberlo hervido, por ejemplo. Es muy importante que los pasos sean una secuencia lógica y ordenada.
Ahora que ya sabemos todos los pasos, mediante el algoritmo, podemos hacer un esquema con estos pasos a seguir. Este esquema será el Diagrama de Flujo.
Un ejemplo para cocinar un huevo para otra persona sería:
- Pregunto si quiere el huevo frito.
- Si me dice que si, lo frio, si me dice que no, lo hago hervido.
- Una vez cocinado le pregunto si quiere sal en el huevo.
- Si me dice que no, lo sirvo en el Plato, si me dice que si, le hecho sal y después lo sirvo en el plato.
Si te fijas los pasos no pueden cambiar su posición. Sería imposible preguntarle si lo quiere frito después de haberlo hervido, por ejemplo. Es muy importante que los pasos sean una secuencia lógica y ordenada.
Ahora que ya sabemos todos los pasos, mediante el algoritmo, podemos hacer un esquema con estos pasos a seguir. Este esquema será el Diagrama de Flujo.
Otro ejemplo de un diagrama de flujo para una operación sencilla. Imaginemos que tenemos una lámpara o bombilla y queremos hacer el diagrama de flujo para saber que hacer cuando la lámpara no funciona.
ACTIVIDAD
Realiza primero el algoritmo y luego representa mediante un diagrama de flujo las siguientes situaciones
1. Tomar café.
2. Sumar dos números y obtener el resultado
3. La suma de los números pares de 1 a 20
SEMANA 4
Operadores lógicos y de comparación en informática
Ingresa al siguiente enlace y realiza la lectura
Observa los siguientes ejemplos de uso de los operadores lógicos



No hay comentarios.:
Publicar un comentario